Flory-Huggins Lattice Theory
of Polymer Solutions,
Part 1
The thermodynamics of (binary) regular polymer solutions1 were first investigated by Paul Flory2 and Maurice Huggins3 independently in the early 1940s. They assumed a rigid lattice frame, that is, the molecules in the pure liquids and in their solution / mixture are considered to be distributed over N0 lattice sites, as illustrated in the figure below. The total number of lattice sites, N0, is assumed to be equal to the number of solvent molecules, Ns, and polymer repeat units, Npr:
N0 = Ns + Npr
where Np is the number of polymer molecules each consisting of r repeat units.
Two-dimensional Lattice
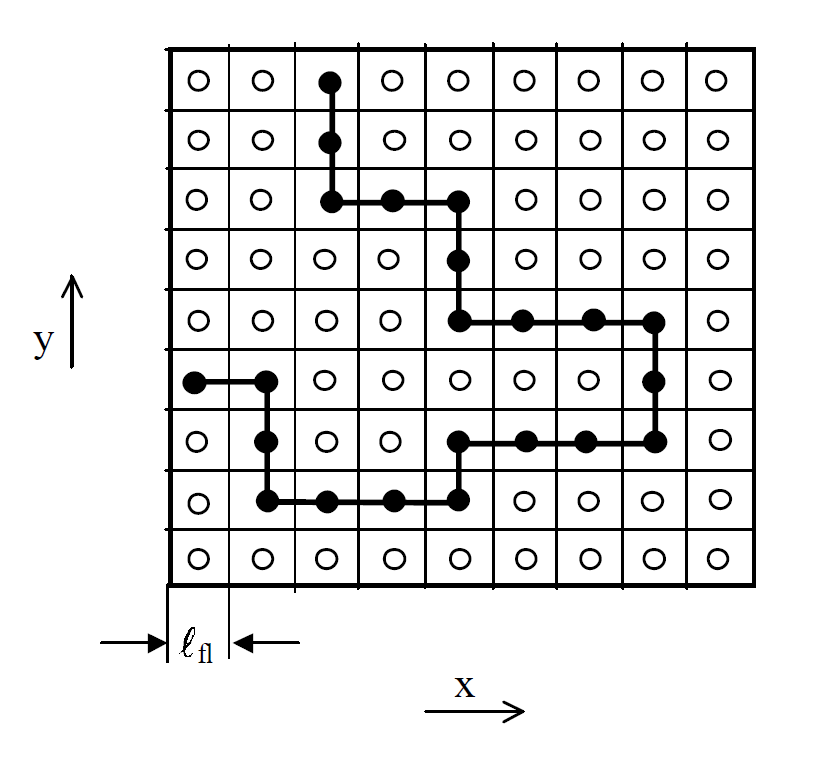
Two-dimensional Lattice
The model has been described in great detail by Flory in his famous book "Principles of Polymer Chemistry" (1953).4 Following the standard theory of mixing for small molecules of similar size and using Stirling's approximation lnM! = M lnM - M, Flory and Huggins obtained following expression for the entropy of mixing:
ΔSmix ≈ -k (Np ln φp + Ns ln φs )
Alternately, the entropy of mixing can be written as
Δsmix = ΔSmix / N0 ≈ -k {φp / (r·vr) · ln φp + φs / vs · ln φs}
where φs and φp are the volume fractions of the solvent and polymer,
φs = Nsvs / (Nsvs + Nprvr), φp = Nprvr / (Nsvs + Nprvr)
and vs and vr are the volumes of a solvent molecule and of a polymer repeat unit, respectively. Obviously, the solvent needs not necessarily to be made of a single unit. The solvent may, in fact, consist of several repeat units or of another polymer.
The Gibbs free energy of mixing6, ΔGmix, includes an enthalpy part, that is, mixing can be an endothermic or an exothermic process
ΔGmix ≈ ΔFmix = ΔUmix - T ΔSmix
where ΔUmix is the heat of mixing. Flory and Huggins introduced a new parameter, the so called Flory-Huggins interaction parameter to describe the the polymer-solvent interaction:5
χps = ΔUmix / (kT Ns φp)
which combined with the entropy term leads to the free energy of mixing:
ΔFmix / kT = Np ln φp + Ns ln φs + χps Ns φp
Assuming equal lattice volumes for both repeat units, the free energy per lattice site can be written
Δfmix / kT ≈ φp / r · ln φp + φs ln φs + χps φs φp
A more general expression for the free energy of mixing is
Δfmix / kT = φp / (r·vr) · ln φp + φs / vs · ln φs + χps φs φp / √(vrvs)
where Δf'mix is the free energy of mixing per unit volume. These equations are the starting point for many other important equations. For example, the partial molar free energy of mixing (chemical potential) can be obtained by differentiation of the expression above with respect to Ns. This gives
Δμs/RT = ln [1- φp] + (1 - 1/r) φp + χps φp2
where μs is the chemical potential of the solvent per mole. Substitution of this expression into the osmotic pressure relation Π = - Δμs / Vs gives
Π ≈ RT Vs-1 · {ln [1- φp] + φp + χpsφp2}
where Vs is the molar volume of the solvent.
References & Notes
The word regular implies that the molecules mix in a totally random manner. Thus, there is no segregation or preference of any molecule for another molecule.
- P. J. Flory, J. Chem. Phys. 9, 660 (1941); 10, 51 (1942)
- M. L. Huggins, J. Phys. Chem. 46, 151 (1942); J. Am. Chem. Soc. 64, 1712 (1942)
- Paul L. Flory, Principles of Polymer Chemistry, Ithaca, New york, 1953
This equation can be easily deduced; The total number of contacts between a polymer and its neighbors is z-2 per chain. The probability that a cell is occupied by a solvent molecule is equal to its volume fraction φs. Then the total number of solvent-monomer contacts is simply (z-2) rNpφs. If εps is the change in energy for the formation of an unlike pair contact, Δεps = εps - ½ (εpp + εss), then the total enthalpy of mixing is simply ΔHmix = Δεps (z-2) rNpφs = Δεps z Nsφp. This is the well-known van Laar equation for mixing for 2-component mixtures, which can be recast to ΔHmix = kT χ Nsφp, with χ = z Δεps / kT.
This quantity is the Helmholz energy when the change in volume upon mixing polymer and solvent molecules is negligible. Then ΔG = ΔH - TΔS = ΔU + pΔV - TΔS reduces to ΔF = ΔU - TΔS.